1 关于逻辑回归
计算的目的不在于数字，而在于洞察事物。
经过了漫长的数据预处理和特征工程过程，终于到了数据建模阶段。正如上面那句话：计算的真正目的不在于数字，而在于洞察事物。这句话其实也可以非常好地诠释我们为何要建立模型了。我们建立模型的目的就是为了洞察数字背后蕴含的事物。
适用于评分卡的模型比较多，如逻辑回归、线性回归、决策树等。逻辑回归是最常用的一种模型，这大概与它的算法的简单易用与模型结果的可解释性有较大的关系。虽然逻辑回归模型比较容量理解，还是再来温习两个概念：回归分析和逻辑回归。
在统计学中，回归分析（regression analysis）指的是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。回归分析按照涉及的变量的多少，分为一元回归和多元回归分析；按照因变量的多少，可分为简单回归分析和多重回归分析；按照自变量和因变量之间的关系类型，可分为线性回归分析和非线性回归分析。
在大数据分析中，回归分析是一种预测性的建模技术，它研究的是因变量（目标）和自变量（预测器）之间的关系。这种技术通常用于预测分析，时间序列模型以及发现变量之间的因果关系。例如，司机的鲁莽驾驶与道路交通事故数量之间的关系，最好的研究方法就是回归。
from 百度百科
而Logistic Regression逻辑回归则是用于预测的回归分析的一种技术或者方法，用来计算”事件成功（Event)”和”事件失败(non-event)”的概率，即可以通过输入的自变量来预测目标变量发生的概率。
odds= p(event)/ (1-p(event)) = probability of event occurrence/probability of not event occurrence
odds 这个公式很熟悉对不对？我们在上一篇文章中提到的证据权重（woe)的计算公式正基于这个比值来的。
woe = ln(odds) = ln(p/(1-p))
logit(p) = ln(p/(1-p)) =b0+b1X1+b2X2+b3X3….+bkXk
上述式子中，p表述具有某个特征的概率。之所以要在公式中使用对数log，是因为在这里我们使用的是的二项分布（因变量），我们需要选择一个对于这个分布最佳的连结函数。它就是Logit函数。在上述方程中，通过观测样本的极大似然估计值来选择参数，而不是最小化平方和误差（如在普通回归使用的）,而且如此以来，我们还可以将目标变量”事件成功（Event)”的概率的取值设置在（0，1）之间。
\(logit(p) = ln(\frac{p(event)}{p(non-event))}) =β_0+β_1X_1+β_2X_2+ β_3x_3....+β_kX_k\)
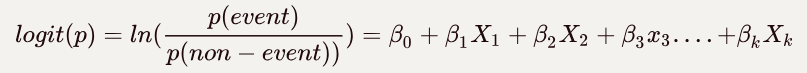
2 建立逻辑回归模型
我们在评分卡建模（二）特征工程中最终筛选出了7个变量作为我们模型入模变量，再来看一下这7个变量：
| 变量编号 | 变量名 | iv值 |
|---|---|---|
| x9 | NumberOfTime30-59DaysPastDueNotWorse | 1.00295 |
| x8 | Debt | 1.00295 |
| x3 | RevolvingUtilizationOfUnsecuredLines | 0.89019 |
| x10 | NumberOfTime60-89DaysPastDueNotWorse | 0.23158 |
| x11 | NumberOfTimes90DaysLate | 0.23158 |
| x1 | Age | 0.23158 |
| x4 | NumberOfOpenCreditLinesAndLoans | 0.08671 |
如此以来，我们就可以将我们的逻辑回归模型表示如下：
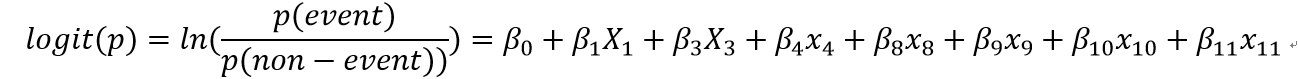
这个公式就是我们建立的逻辑回归模型了。因为我们的目标是要做一个信用评分卡，好客户打分越高，坏客户打分越低。所以这里注意一点：
p(event) = p(好客户)
所以，这我们在计算woe时也要特别注意一点，要与这个是一致的,即:
woe = ln(p(好客户)/p(坏客户))
3 参数估计
3.1 训练集与测试集划分
我们现在的目的已经很明确了：建立一个预测模型，以准确地预测客户是好客户还是坏客户，即预测客户会不会违约。
再来看两个术语：训练误差和泛化误差。
训练误差，training error, 又叫经验误差，指模型在训练集上实际预测输出与训练样本真实输出之间的误差。
泛化误差， generalization error ,批模型在新样本上的实际预测输出与训练样本真实输出之间的误差。
显然，我们希望得到一个泛化误差小的预测模型，但实际上我们在建立模型时对新样本却是不可知的，使用到的所谓训练数据其实都是历史数据，为了可以得到在新样本上表现较好的模型，就需要从训练样本中尽可能地探究样本的普遍规律，这样在对新样本进行预测时才可以尽可能地作出正确的预测，但是如果模型把训练样本学得过好地时候，就有可能把训练样本自身的一些特点当作了潜在样本都会具有的规律，这样就会导致泛化性能下降，导致过拟合(overfitting)；或者模型把训练样本学得太差，也会导致泛化性能下降，导致欠拟合(underfitting)。
所以，在使用模型训练数据时， 需要先划分训练集与测试集，通过模型在测试集上表现来评估模型对新样本的预测能力，模型在测试集上的测试误差可以近似地看作泛化误差。
训练集和测试集的划分方法一般有留出法、交叉验证法和自助法，详情可以参考https://blog.csdn.net/c369624808/article/details/78408047
在这里使用直接使用sklearn提供的train_test_split方法，按照3：7的比例将数据集随机划分为互斥的测试集和训练集，关于train_test_split的使用方法及解释，可以参考官方文档。
1
2
3
4
5
from sklearn.model_selection import train_test_split
# 逾期超过90天的人，0代表否（即好客户），1代表是（即坏客户）
y = df['SeriousDlqin2yrs']
X_train, X_test, y_train, y_test= train_test_split(df, y, test_size=0.3, random_state=10)
3.2 原始变量woe编码转换
逻辑回归模型建立后，我们就要使用上面划分后的训练数据对我们在模型中设定的参数进行参数估计。
βi可以衡量变量对违约率的影响，逻辑回归模型的参数是用极大似然法来估计我们模型中设定的每个参数值(βi)。
另外，一般而言，因为各个变量之间的量纲不一样，例如age列的值在20-100之间，负债额Debt的取值却在0~10万之间变动 ，对于逻辑回归中的自变量要先进行数据归一化，否则原始变量容易导致模型稳定型不佳。
不过，因为我们是用于开发评分卡，所以这里采用每一个变量分组后的woe值作为入模变量的取值，woe值是一个对数值，在0~1之间，从而可以有效避免变量值中出现的 极端值的情形，也可以减少模型过度配适的现象,以下是最终放入模型的用woe值替换原始变量后的数据示例：
| x1_woe | x3_woe | x4_woe | x8_woe | x9_woe | x10_woe | x11_woe |
|---|---|---|---|---|---|---|
| -0.225 | -1.055 | -1.538 | -0.029 | 0.215 | 0.246 | 0.146 |
| -0.261 | -1.055 | 0.355 | -0.029 | 0.215 | 0.246 | 0.146 |
| 1.061 | 1.161 | 0.028 | -0.029 | 0.215 | 0.246 | 0.146 |
| 1.061 | 1.161 | 0.028 | -0.029 | 0.215 | 0.246 | 0.146 |
| -0.118 | 1.161 | 0.028 | -0.029 | -1.603 | 0.246 | 0.146 |
| -0.225 | -1.055 | 0.028 | -0.029 | 0.215 | 0.246 | 0.146 |
3.3 逻辑回归结果
| B | S.E. | Wald | 自由度 | 显著性 | Exp(B) | |
|---|---|---|---|---|---|---|
| age_woe | -.549 | .034 | 254.163 | 1 | .000 | .578 |
| RevolvingUtilizationOfUnsecuredLines_woe | -.705 | .017 | 1734.589 | 1 | 0.000 | .494 |
| NumberOfOpenCreditLinesAndLoans_woe | -.402 | .042 | 92.267 | 1 | .000 | .669 |
| Debt_woe | -.633 | .134 | 22.415 | 1 | .000 | .531 |
| NumberOfTime3059DaysPastDueNotWorse_woe | -.599 | .020 | 899.287 | 1 | .000 | .549 |
| NumberOfTime6089DaysPastDueNotWorse_woe | -.561 | .018 | 958.404 | 1 | .000 | .570 |
| NumberOfTimes90DaysLate_woe | -.566 | .020 | 816.763 | 1 | .000 | .568 |
| 常量 | -2.749 | .016 | 30627.956 | 1 | 0.000 | .064 |
这个结果就是我们的逻辑回归结果了，表格中的B为回归系数，S.E.为STD ERR的缩写，表示估计标准误，Wald是一个用于估计回归系数显著性(P)的统计量。这个结果是用spss完成的，spss的回归分析结果更容易理解一些，实际上在编程操作时是使用了第三方库statsmodels来搭建模型的。模型输出的结果如下所示：
| Dep. Variable: | SeriousDlqin2yrs | No. Observations: | 100940 |
|---|---|---|---|
| Model: | Logit | Df Residuals: | 100932 |
| Method: | MLE | Df Model: | 7 |
| Date: | Thu, 22 Nov 2018 | Pseudo R-squ.: | 0.1997 |
| Time: | 15:02:23 | Log-Likelihood: | -18108 |
| converged: | TRUE | LL-Null: | -22625 |
| LLR p-value: | 0 |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | -2.7493 | 0.016 | -175.008 | 0 | -2.78 | -2.719 |
| age_woe | -0.5487 | 0.034 | -15.943 | 0 | -0.616 | -0.481 |
| RevolvingUtilizationOfUnsecuredLines_woe | -0.7053 | 0.017 | -41.648 | 0 | -0.738 | -0.672 |
| NumberOfOpenCreditLinesAndLoans_woe | -0.4017 | 0.042 | -9.606 | 0 | -0.484 | -0.32 |
| Debt_woe | -0.6329 | 0.134 | -4.734 | 0 | -0.895 | -0.371 |
| NumberOfTime30-59DaysPastDueNotWorse_woe | -0.5992 | 0.02 | -29.988 | 0 | -0.638 | -0.56 |
| NumberOfTime60-89DaysPastDueNotWorse_woe | -0.5615 | 0.018 | -30.958 | 0 | -0.597 | -0.526 |
| NumberOfTimes90DaysLate_woe | -0.5658 | 0.02 | -28.579 | 0 | -0.605 | -0.527 |
coef 表示回归系数，或者叫参数估计值，p>|z|表示参数显著性，[0.025,0.975]表示参数估计值的置信区间。
对比spss回归结果与statsmodels的回归结果来看，虽然呈现形式上有差异，但结果都是一致的，而且模型中的每个参数都是显著的，单单从模型的角度来说，没有变量需要被排除出模型。
另外，要注意的是这里使用的不是原始变量，是原始变量woe编码，结合woe越大，好客户占比越多；woe值越小，坏客户占比越多我们可以初步得到以下结论：
- 年龄_woe与坏客户之间负相关，即年龄变量的woe值越大，客户违约的可能性就越小；年龄变量的woe值越小，客户违约的可能性就越大；
- 逾期次数woe与坏客户之间负相关，即逾期次数woe值越大，违约的可能性越小
- ……
如果还要进一步分析各个变量与违约可能性之间的显著关系，还要结合各个变量的woe值单调性来解释，限于篇幅，不在这里过多地解释。
于是根据我们之前设定的逻辑回归模型，预测客户是否是好客户的回归模型就可以这样写了：
\(logit(p) = ln(\frac{p(event)}{p(non-event))}) =-2.749 - 0.549*age -0.705*RevolvingUtilizationOfUnsecuredLines - 0.402*NumberOfOpenCreditLinesAndLoans - 0.633*Debt -0.599*NumberOfTime3059DaysPastDueNotWorse-0.561*NumberOfTime6089DaysPastDueNotWorse - 0.569*NumberOfTimes90DaysLate\)
4 模型评估
4.1 模型度量的几个术语
查准率和查全率
逻辑回归模型训练完成后，我们就可以通过对我们上面划分的测试集的预测结果来评估模型的性能了。
从逻辑回归模型可以看出，逻辑回归模型的预测结果差不是某个事件是否发生，而是事件发生的概率，具体到我们建立的模型而言，我们的预测变量是SeriousDlqin2yrs,即客户逾期天数是否超过90天，模型输出的结果就是预测客户是否会逾期超过90天，即预测客户是好客户还是坏客户。
先来看一下根据SeriousDlqin2yrs二分类变量分类结果的混淆矩阵：
| 真实情况 | 预测为好客户 | 预测为坏客户 |
|---|---|---|
| 好客户 | 真正例 TP(True Positive) | 假反例 FN(False Negative) |
| 坏客户 | 假正例 FP(False Positive) | 真反例 TN(True Negative) |
简单解释一下：
真正例：样本本身为好客户，预测结果也为好客户，预测正确!
假正例：样本本身为坏客户，预测结果却为好客户，预测错误，将坏客户预测成好客户了
真反例：样本本身为坏客户，预测结果也为坏客户，预测正确！
假反例：样本本身为好客户，预测结果却为坏客户，预测错误，却将好客户预测成了坏客户。
再来看查准率 和查全率的定义：
查准率 P = TP/(TP + FP)
查全率 R = TP/(TP +FN)
查准率和查全率这两个概念如果初次接触，还是比较容易让人困惑的，简单来说：
查准率是针对预测结果而言的，表示预测结果中有多少正例是预测正确的；具体到我们本次的模型而言，就是模型对测试样本的预测结果中，被预测为好客户的样本中有多少好客户是被预测正确的。
查全率是针对测试样本而言的，表示测试样本中有多少正例是被预测正确的；具体到我们本次的模型而言，就是模型对测试样本的预测结果中，实际为好客户的样本中有多少好客户是预测正确的。
查准率和查全率是一对矛盾的度量，一般来说，查准率高了，查全率就会低；反之，查全率高了，查准率就会低，此消彼长，至于为什么查全率和查准率会此消彼长呢？单单从概念上还真的不能直观地看出来，先抱着拿来主义的思想，姑且先这样记着这个结论吧。
ROC 与 AUC
受试者工作特征曲线 （receiver operating characteristic curve，简称ROC曲线），又称为感受性曲线（sensitivity curve）。得此名的原因在于曲线上各点反映着相同的感受性，它们都是对同一信号刺激的反应，只不过是在两种不同的判定标准下所得的结果而已。受试者工作特征曲线就是以假阳性概率（False positive rate）为横轴，真阳性概率（True positive rate）为纵轴所组成的坐标图，和受试者在特定刺激条件下由于采用不同的判断标准得出的不同结果画出的曲线。
ROC曲线最早是运用在军事上，后来逐渐运用到医学领域。相传在第二次世界大战期间，雷达兵的任务之一就是死死地盯住雷达显示器，观察是否有敌机来袭。理论上讲，只要有敌机来袭，雷达屏幕上就会出现相应的信号，但是实际上，有时如果有飞鸟出现在雷达扫描区域时，雷达屏幕上有时也会出现信号。这种情况令雷达兵烦恼不已：如果过于谨慎，凡是有信号就确定为敌机来袭，显然会增加误报风险；如果过于大胆，凡是信号都认为飞鸟，又会增加漏报的风险。每个雷达兵都竭尽所能地研究飞鸟信号和飞机信号之间的区别，以便增加预报的准确性。但问题在于，每个雷达兵都有自己的判别标准，有的雷达兵比较谨慎，容易出现误报；有的雷达兵则比较胆大，容易出现漏报。
为了研究每个雷达兵预报的准确性，雷达兵的管理者汇总了所有雷达兵的预报特点，特别是他们漏报和误报的概率，并将这些概率画到一个二维坐标里面。这个二维坐标的纵坐标为敏感性，即在所有敌机来袭的事件中，每个雷达兵准确预报的概率。而横坐标则为特异性，表示了在所有非敌机来袭信号中，雷达兵预报错误的概率。由于每个雷达兵的预报标准不同，且得到的敏感性和特异性的组合也不同。将这些雷达兵的预报性能进行汇总后，雷达兵管理员发现他们刚好在一条曲线上，这条曲线就是我们经常在医学杂志上看见的ROC曲线。
通过以上资料，对ROC曲线有了初步的认知，ROC曲线的横坐标为假阳性率（False Positive Rate，FPR）；纵坐标为真阳性率（True Positive Rate，TPR）。FPR和TPR的计算方法分别为：
1
2
真阳性率 TPR = TP/(TP+FN)
假阳性率 FPR= FP/(TN+FP)
为了便于理解，可以再结合分类结果的混淆矩阵来看：
| 真实情况 | 预测为好客户 | 预测为坏客户 |
|---|---|---|
| 好客户 | 真正例TP(True Positive) | 假反例FN(False Negative) |
| 坏客户 | 假正例FP(False Positive) | 真反例TN(True Negative) |
可以看出来，对于真阳性率TPR其实就是查全率，它表示测试样本中有多少好客户是被正确预测的，却衡量模型准确程度的指标；而假阳性率则表示测试样本中有多少坏客户是被错误预测的，即衡量模型错误程度的指标。
显然地，真阳性率 越高越好，假阳性率则越低越好。
再来看下AUC的概念，AUC指的是ROC曲线下的面积大小，该值能够量化地反映基于ROC曲线衡量出的模型性能。计算AUC值只需要沿着ROC横轴做积分就可以了。由于ROC曲线一般都处于y=x这条直线的上方（如果不是的话，只要把模型预测的概率反转成1−p就可以得到一个更好的分类器），所以AUC的取值一般在0.5～1之间。AUC越大，说明分类器越可能把真正的正样本排在前面，分类性能越好。
另外要注意的是，AUC的取值完全取决于模型本身，因此AUC可以被视作评估逻辑回归的比较合理全面地指标。
4.2 模型度量
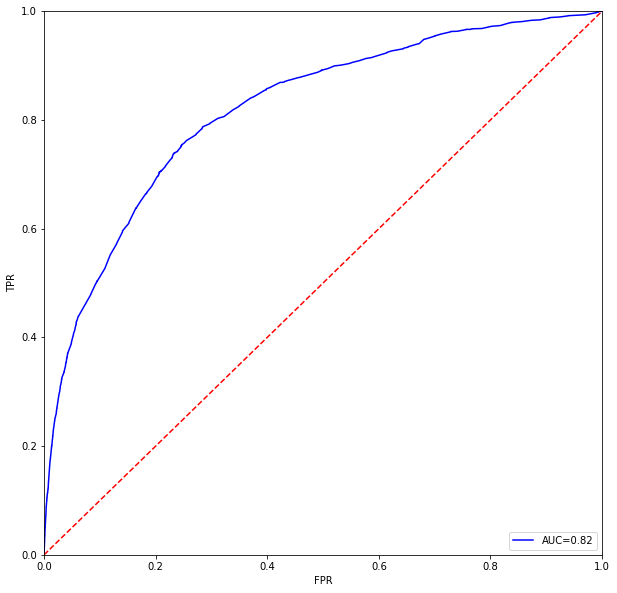
上图即是本次逻辑回归模型的ROC曲线图，可以看到，本次逻辑回归模型的AUC值为0.82，可以理解为模型预测正确的概率为0.82,这个结果其实也还可以。
##5 结语
因为这个建模仅仅是作为学习和研究之用，所以就不再深入研究，关于评分卡的逻辑回归建模至此也就结束了。
但这个逻辑回归产出的模型是一个回归式，在评分卡的运用上并不是很容易理解 ，因此需要将变量转换为分数以利于业务上的运用。关于最终模型的产出结果请见下一篇文章。
