引言
通常而言,特征变量要经过从长变量列表(long list) 到短变量列表(short list)的过程。其实这个过程的核心就是特征工程了。
长列表就是在评分卡模型开发之前,数据源提供方将与业务相关的数据中所有变量列为一个长变量列表,供建模时选用。顾名思义,这个长变量列表会非常长,里面的变量甚至有成百上千个,实际进行评分卡建模时不可能全部使用。这个时候就会根据实际业务对特征变量进行分析以筛选出入模变量。
对长变量列表筛选完成后,我们会将这个变量放入一个短变量列表,实际建模时就可以直接使用短变量列表中的变量作为入模变量。
另外,如果长变量列表里变量非常非常多,也可以考虑设置一个过渡变量列表(middle list),先将明显与业务不契合的变量剔除后放进过渡变量列表,模型开发人员再根据这个过渡变量列表进行特征筛选。
其实,本案例的数据源(www.kaggle.com:GiveMeSomeCredit)提供的数据字典就可以看作是一个过渡变量列表(middle list),我们拿到的其实并不是源数据,而是经过Kaggle数据源提供方筛选处理后的数据以及变量列表。
言归正传,让我们回到特征工程这一概念上来,遵循 what how why三步曲的步骤,先来看一下什么是特征工程。
1 特征工程的定义
Feature engineering is the process of using domain knowledge of the data to create features that make machine learning algorithms work.
以上是维基百科对Feature engineering的定义,翻译一下:
特征工程是基于既定数据的专业领域知识或经验去创建特征以使机器学习算法工作的过程。
这个定义在我看来还是相对比较权威和准确的。特征工程是机器学习应用的基础,通过特征工程我们将对样本数据中的变量进行筛选,并根据具体的业务场景构建一些衍生变量。
一般而言,特征(Feature)就是我们在进行数据分析中使用到的数据的特性或者属性,只要对数据分析有用的任何特性或者属性都可以作为特征(Feature)。具体而言,特征(Feature)其实就是我们使用到的样本数据中的变量或者基于这些变量而构建的衍生变量。*
明确了特征的概念,那么特征工程的概念就很容易理解了。特征工程其实就是目的是我们从原始数据中提取特征以供算法和模型使用的一个过程。通常数据预处理也应该是特征工程里的特征处理的一个步骤,不过为了写博客的方便和便于查看,人为地把数据预处理单独作为一个步骤来讲了。
2 特征衍生
一般而言,特征衍生即变量衍生。
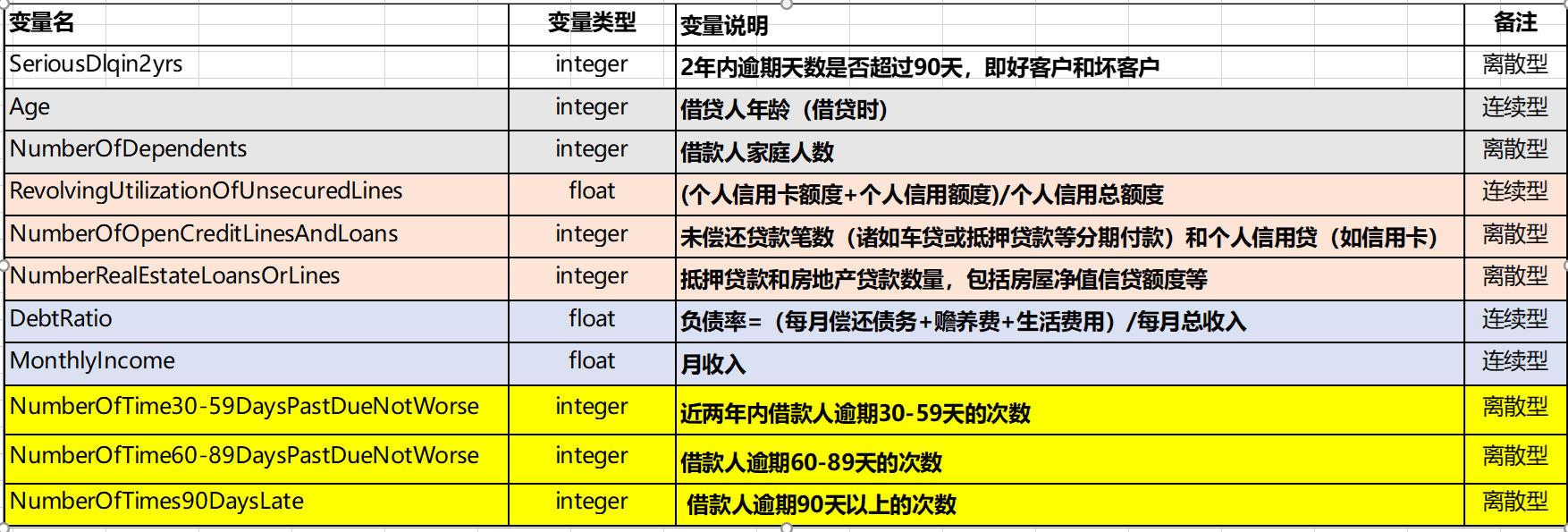
从数据的原始变量的数据字典里可以看到,样本数据共有11个原始变量,其中SeiousDlqin2yrs(即好坏客户)将作为因变量,剩余的10个变量可以作为自变量。
经过对数据原始变量的分析,我们构建了两个衍生变量:Debt和NumberOfPastDue,具体如下:
| 变量名 | 变量说明 | 备注 |
|---|---|---|
| Debt | =DebtRatio * MonthlyIncome,即个人负债额 | 连续型 |
| NumberOfPastDue | =NumberOfTime30-59DaysPastDueNotWorse+NumberOfTime60-89DaysPastDueNotWorse+NumberOfTimes90DaysLate,即借款人逾期次数之和 | 离散型 |

3 特征选取
本次评分卡建模是学习探索性质的,原始数据是来自于 www.kaggle.com:GiveMeSomeCredit, 实际上kaggle在发布这个数据前已经是经过特征选取了,实际上在基于业务建模时,获取到的原始数据 通常会有成百上千个维度,不可能把这些维度全部作为变量放入模型中去,这个时候就需要我们使用一些方法去选取变量了。
一般而言,选取入模变量的过程也是个比较复杂的过程,需要考虑的因素很多,如变量的预测能力、变量之间的相关性、变量在业务上的可解释性等。但是,其中最核心的衡量标准其实就是变量的预测能力。
“变量的预测能力”一般而言是要通过一定的方法来量化,不能拍脑袋说某个变量预测能力强,要有数据来支撑,那这个时候就要借助统计学了。现在看来当时当时在学校时真的就应该学习好这门课程。
我们现在需要做的就是去找一个方法,将我们本次数据中的各个变量的变量的预测能力通过某一个数据指标来进行量化。
IV就是这样一种指标,他可以用来衡量自变量的预测能力。类似的指标还有信息增益、基尼系数等等。 IV的全称是Information Value,即信息价值,它依赖于WOE(证据权重)。 关于IV和WOE这两个指标可以参考CSDN上的一篇文章:评分卡模型中的IV和WOE详解
下面我们将使用这一IV这一指标,对我们经过数据预处理后的12个变量进行特征选取。
3.1 特征分箱
特征分箱也可叫变量分箱其实就是对各个特征变量进行分组,以期找出最好的分组方式。
特征分箱根据模型变量的类型也可以分为两个类型:
- 连续型变量(Continous Variable)分箱:一般是通过最优算法对连续型变量进行离散化并分箱
- 离散型变量(Discrete Variable)分箱:一般是对离散型变量进行合并,减少分箱数量
信用评分卡建模中一般有常用的特征分箱方法有等距分箱、等深分箱、最优分箱。本文使用最优分箱方法。
初次接触评分卡时对特征分箱这个概念并不是很理解,翻看了很多相关的参考资料后,在我看来,特征分箱其实就是对变量进行分组,针对不同的分组设置不同的评分规则。
举例来说,对于年龄(age)这个变量,在21~100之间变动,我们通过数据分析发现不同年龄段的人群违约率差别较大,那么我们在开发评分卡时就不能针对所有年龄段设置同样的打分,要把年龄分成几段来打分,比如说25岁以下的打多少分,25-40岁的打多少分,40-60岁的打多少分等等。
那么我们特征分箱的目的之一就是要确定一个科学的分组规则,即我们将年龄分为几组,每组打多少分。
那如果变量的科学分组规则只是特征分箱的唯一目的,我们大可以在完成变量筛选之后再来解决这个问题,如此以来也避免了对一些即将被剔除的变量做无用功。所以说确定变量的科学分组规则只是特征分箱的目的之一。特征分箱的另外一个非常重要的目的就是计算变量预测能力。

在进行特征分箱前,我们先对变量进行分析编号,区别出离散型变量和连续型变量,因为这两类变量的最分箱方法并不相同,主要分箱原则如下:
- 对于连续型变量,通过IV值进行分箱,得到一个IV值最优的分箱结果
- 对于离散型变量,通过卡方最优分箱,合并卡方值相近的分箱,以降低分箱数量。
下面,我们对数据中既定的变量进行编号,编号规则如下所示。
| 编号 | 变量名 | 备注 |
|---|---|---|
| y | SeriousDlqin2yrs | 离散型 |
| x1 | age | 连续型 |
| x2 | NumberOfDependents | 离散型 |
| x3 | RevolvingUtilizationOfUnsecuredLines | 连续型 |
| x4 | NumberOfOpenCreditLinesAndLoans | 离散型 |
| x5 | NumberRealEstateLoansOrLines | 离散型 |
| x6 | DebtRatio | 连续型 |
| x7 | MonthlyIncome | 连续型 |
| x8 | Debt | 连续型 |
| x9 | NumberOfTime30-59DaysPastDueNotWorse | 离散型 |
| x10 | NumberOfTime60-89DaysPastDueNotWorse | 离散型 |
| x11 | NumberOfTimes90DaysLate | 离散型 |
| x12 | NumberOfPastDue | 离散型 |
3.1.1 连续变量最优分箱
定义基于Information Value对连续变量进行最优分箱的计算函数,通过IV最大进行分箱,并确定每个连续变量的最优分箱结果。这里不再贴代码,详细可以参考:[对数据集进行最优分箱和WOE转换](https://www.cnblogs.com/leixingzhi7/p/9366908.html)
3.1.2 离散变量最优分箱
对离散型变量采用自底向上的(即基于合并的)数据离散化方法。它依赖于卡方检验:具有最小卡方值的相邻区间合并在一起,直到满足确定的停止准则。
卡方分箱基本思想:对于精确的离散化,相对类频率在一个区间内应当完全一致。因此,如果两个相邻的区间具有非常类似的类分布,则这两个区间可以合并;否则,它们应当保持分开。而低卡方值表明它们具有相似的类分布。
主要算法如下:

定义基于卡方分箱的离散型变量最优分箱的计算函数,同样地这里也不再贴代码,详细可以参考:评分卡系列(二):特征工程
3.1.3 变量分箱结果与分析
变量的最终分箱结果一般应满足以下几项原则:
- 变量分箱后的woe值一般须是单调的
- 单个变量最多分8箱
- 各变量分组的好坏对比值(即good/bad)至少需差距15以上
- 各变量分组须涵盖2%以上的模型开发样本
- 各变量分组至少有30个发生目标事件的开发样本或开发样本至少占该组样本的1%。
—单良、乔杨著《数据化风控-信用评分卡建模教程》
以上是《数据化风控-信用评分卡建模教程》一书中提到的变量分箱结果应满足的几个原则。
但这几个原则只是一个参考,实际中还要根据业务需求进行调整。比如说变量分箱后的woe值一般要是单调的,之所以这样规定是因为逻辑回归对于线性可分的数据,预测效果会更佳,但是如果不单调,业务上可以解释得通,也不一定必须要是单调的。
本次谈到分箱共涉及12个变量,其中7个非连续变量,5个连续变量。
限于篇幅还有时间,以及本评分卡建模的目的只是为了学习研究,并非用于实际业务,这里只取一个连续变量和一具非连续变量来作示例说明,剩余的10个变量,仅展示结果,不作说明。
3.1.3.1 连续型变量age分箱结果分析
| group | min | max | bad | good | bad_rate | woe | iv |
|---|---|---|---|---|---|---|---|
| 21~34 | 21 | 34 | 1733 | 16227 | 0.0964922 | -0.5301875 | 0.04434118 |
| 35~40 | 35 | 40 | 1225 | 13933 | 0.08081541 | -0.3356907 | 0.01375186 |
| 41~45 | 41 | 45 | 1171 | 14350 | 0.07544617 | -0.2611181 | 0.00824075 |
| 46~50 | 46 | 50 | 1322 | 16796 | 0.07296611 | -0.225015 | 0.00702931 |
| 51~54 | 51 | 54 | 920 | 13014 | 0.06602555 | -0.1176027 | 0.00140779 |
| 55~59 | 55 | 59 | 818 | 15690 | 0.04955173 | 0.18690653 | 0.00368489 |
| 60~64 | 60 | 64 | 628 | 15941 | 0.03790211 | 0.46709954 | 0.02048107 |
| 65~71 | 65 | 71 | 377 | 14419 | 0.02547986 | 0.87704689 | 0.054434 |
| 72~99 | 72 | 99 | 333 | 15303 | 0.02129701 | 1.0606517 | 0.07821335 |
以上是变量age的分箱结果,实际在对age分箱时使用了最优化分箱算法,指定最大分箱数量为10个。经过运算,算法最后给出了这9个分箱结果。
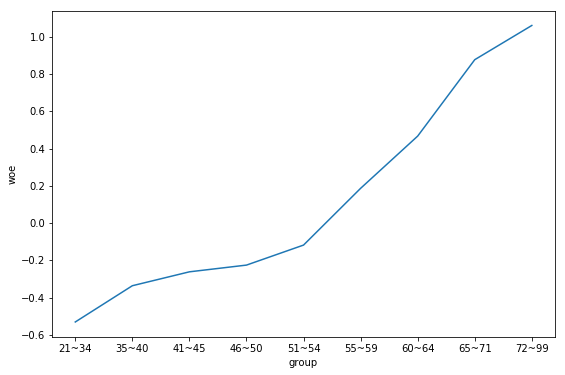
上图是age各个分组的woe值的线型变化图。再来看下woe值的计算方法:WOE=log(好客户比例/坏客户比例)可以把woe值看作好坏客户的优势比。
先来温习下高数知识:ln是以10为底的常用对数,是一个单调递增函数,即好客户比例/坏客户比例越大,woe越大,也就是说,对于每个分组,好客户越多,woe值越大。
弄清楚了woe值的计算方法,再来看这个age分组的woe变化图,可以很容易看出以下几点:
- 分箱后的woe值是单调的
- 年龄越大的客户分组中,好客户占比越多。
这也与我们的常识认知是一致的,21-34岁的群体正是社会最年经的成人群体,消费能力正是最旺盛的时候,而且这个年龄的人大部分都是未婚,违约成本相对较低。
综合以上,我们可以认为这个分组是合理的,因此不作调整。
3.1.3.2 离散型变量NumberOfTime30-59DaysPastDueNotWorse分箱结果分析
| group | min | max | bad | good | bad_rate | woe | iv |
|---|---|---|---|---|---|---|---|
| 0~1 | 0 | 1 | 4612 | 91637 | 0.04791738 | 0.21932877 | 0.04167172 |
| 2~2 | 2 | 2 | 701 | 2207 | 0.24105915 | -1.6229632 | 0.1534041 |
| 3~3 | 3 | 3 | 321 | 691 | 0.31719368 | -2.003146 | 0.09344218 |
| 4~4 | 4 | 4 | 169 | 262 | 0.39211137 | -2.331399 | 0.05975556 |
| 5~12 | 5 | 12 | 150 | 190 | 0.44117647 | -2.533456 | 0.05876885 |
以上是离散型变量NumberOfTime30-59DaysPastDueNotWorse分箱结果,这个结果是基于卡方最优分箱算法。看下分组后的woe值的线性变化:
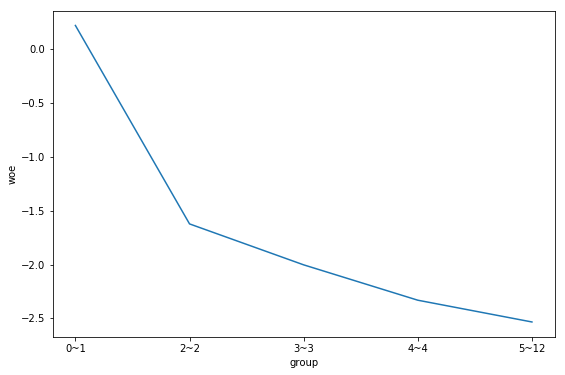
NumberOfTime30-59DaysPastDueNotWorse指近两年内借款人逾期30-59天的次数。在对这个变量的woe值的线性变化图分析之前,再来明确一点:woe值越大,分组中的好客户占比越多;反之,woe值越小,分组中坏客户占比越多。
再来分析这个线性变化图也可以很容易地发现两点:
- 第一,这个woe值是单调递减的
- 第二,逾期次数越多的分组群体中坏客户占比越多
其实这两点通过常识认知也是可以很容易进行解释:一般逾期0~1次的客户一般比较爱惜自己的羽毛,逾期通常是因为忘记还款日或者其他特殊原因,在收到逾期提醒时一般会履约还款;而那些逾期将数过多的,排除部分骗贷群体,通常是自身的还款能力较弱,无法履行约定按期还款。
综合以上,我们也认为这个变量的分箱结果是合理的,可以作为入模变量。
3.1.3.3 其他变量的分箱结果
- x2:
NumberOfDependents借款人家庭人数分箱结果
| group | min | max | bad | good | bad_rate | woe | iv |
|---|---|---|---|---|---|---|---|
| 0.0~0.0 | 0.0 | 0.0 | 3057 | 57002 | 0.051 | 0.156 | 0.01350657 |
| 1.0~2.0 | 1.0 | 2.0 | 2131 | 29800 | 0.067 | -0.132 | 0.00584016 |
| 3.0~3.0 | 3.0 | 3.0 | 523 | 5827 | 0.082 | -0.359 | 0.00951696 |
| 4.0~4.0 | 4.0 | 4.0 | 178 | 1783 | 0.091 | -0.466 | 0.00518653 |
| 5.0~20.0 | 5.0 | 20.0 | 64 | 575 | 0.1 | -0.574 | 0.00269632 |
- x3:
RevolvingUtilizationOfUnsecuredLines(个人信用卡额度+个人信用额度)/个人信用总额度分箱结果
| group | min | max | bad | good | bad_rate | woe | iv |
|---|---|---|---|---|---|---|---|
| 0.0~0.029 | 0.0 | 0.029 | 663 | 35387 | 0.018 | 1.21 | 0.2215179 |
| 0.029~0.143 | 0.029 | 0.143 | 696 | 35354 | 0.019 | 1.161 | 0.20777181 |
| 0.143~0.514 | 0.143 | 0.514 | 1654 | 34396 | 0.046 | 0.268 | 0.0159592 |
| 0.514~1.0 | 0.514 | 1.0 | 5514 | 30536 | 0.153 | -1.055 | 0.44476821 |
- x4:
NumberOfOpenCreditLinesAndLoans未偿还贷款笔数(诸如车贷或抵押贷款等分期付款)和个人信用贷(如信用卡) 分箱结果
| group | min | max | bad | good | bad_rate | woe | iv |
|---|---|---|---|---|---|---|---|
| 0.0~0.0 | 0.0 | 0.0 | 242 | 770 | 0.239 | -1.612 | 0.05246318 |
| 1.0~1.0 | 1.0 | 1.0 | 357 | 2449 | 0.127 | -0.844 | 0.02885407 |
| 2.0~7.0 | 2.0 | 7.0 | 2505 | 42632 | 0.055 | 0.064 | 0.00179348 |
| 8.0~23.0 | 8.0 | 23.0 | 2764 | 47937 | 0.055 | 0.083 | 0.00335032 |
| 24.0~58.0 | 24.0 | 58.0 | 85 | 1199 | 0.066 | -0.123 | 0.00020366 |
- x5 :
NumberRealEstateLoansOrLines抵押贷款和房地产贷款数量,包括房屋净值信贷额度等 分箱结果
| group | min | max | bad | good | bad_rate | woe | iv |
|---|---|---|---|---|---|---|---|
| 0.0~0.0 | 0.0 | 0.0 | 2649 | 34692 | 0.071 | -0.198 | 0.01579185 |
| 1.0~1.0 | 1.0 | 1.0 | 1683 | 34080 | 0.047 | 0.238 | 0.01810498 |
| 2.0~5.0 | 2.0 | 5.0 | 1543 | 25851 | 0.056 | 0.049 | 0.00063484 |
| 6.0~8.0 | 6.0 | 8.0 | 53 | 275 | 0.162 | -1.123 | 0.00674692 |
| 9.0~54.0 | 9.0 | 54.0 | 25 | 89 | 0.219 | -1.5 | 0.00489389 |
- x6:
DebtRatio负债率=(每月偿还债务+赡养费+生活费用)/每月总收入 分箱结果
| group | min | max | bad | good | bad_rate | woe | iv |
|---|---|---|---|---|---|---|---|
| 0.0~0.239 | 0.0 | 0.239 | 2495 | 45572 | 0.052 | 0.138 | 0.00597483 |
| 0.239~0.56 | 0.239 | 0.56 | 2726 | 45340 | 0.057 | 0.044 | 0.0006378 |
| 0.56~5000.0 | 0.56 | 5000.0 | 3306 | 44761 | 0.069 | -0.161 | 0.00930441 |
- x7:
MonthlyIncome月收入 分箱结果
| group | min | max | bad | good | bad_rate | woe | iv |
|---|---|---|---|---|---|---|---|
| 0.0~3300.0 | 0.0 | 3300.0 | 3218 | 45162 | 0.067 | -0.126 | 0.00560896 |
| 3301.0~6735.0 | 3301.0 | 6735.0 | 3167 | 44587 | 0.066 | -0.122 | 0.00521827 |
| 6736.0~100000.0 | 6736.0 | 100000.0 | 2142 | 45924 | 0.045 | 0.298 | 0.02601191 |
- x8:
Debt=DebtRation * MonthlyIncome,即个人负债额 分箱结果
| group | min | max | bad | good | bad_rate | woe | iv |
|---|---|---|---|---|---|---|---|
| 0.0~4122300.0 | 0.0 | 4122300.0 | 8096 | 125071 | 0.061 | -0.029 | 0.00080035 |
| 4125030.0~12369000.0 | 4125030.0 | 12369000.0 | 237 | 6064 | 0.038 | 0.475 | 0.00802828 |
| 12369630.0~20615000.0 | 12369630.0 | 20615000.0 | 52 | 1645 | 0.031 | 0.687 | 0.00414018 |
| 20623246.0~28861000.0 | 20623246.0 | 28861000.0 | 62 | 1540 | 0.039 | 0.445 | 0.00181551 |
| 28869246.0~41230000.0 | 28869246.0 | 41230000.0 | 80 | 1353 | 0.056 | 0.061 | 3.6023E-05 |
- x10:
NumberOfTime60-89DaysPastDueNotWorse借款人逾期60-89天的次数 分箱结果
| group | min | max | bad | good | bad_rate | woe | iv |
|---|---|---|---|---|---|---|---|
| 0.0~0.0 | 0.0 | 0.0 | 4505 | 92003 | 0.047 | 0.247 | 0.0523205 |
| 1.0~1.0 | 1.0 | 1.0 | 1012 | 2524 | 0.286 | -1.856 | 0.26619914 |
| 2.0~2.0 | 2.0 | 2.0 | 294 | 344 | 0.461 | -2.613 | 0.11958477 |
| 3.0~3.0 | 3.0 | 3.0 | 90 | 73 | 0.552 | -2.979 | 0.04274836 |
| 4.0~11.0 | 4.0 | 11.0 | 52 | 43 | 0.547 | -2.96 | 0.0245159 |
- x11:
NumberOfTimes90DaysLate借款人逾期90天以上的次数 分箱结果
| group | min | max | bad | good | bad_rate | woe | iv |
|---|---|---|---|---|---|---|---|
| 0.0~1.0 | 0.0 | 1.0 | 5122 | 94245 | 0.052 | 0.143 | 0.01884481 |
| 2.0~2.0 | 2.0 | 2.0 | 419 | 470 | 0.471 | -2.655 | 0.17373426 |
| 3.0~3.0 | 3.0 | 3.0 | 210 | 151 | 0.582 | -3.1 | 0.10442858 |
| 4.0~4.0 | 4.0 | 4.0 | 103 | 55 | 0.652 | -3.397 | 0.05680862 |
| 5.0~17.0 | 5.0 | 17.0 | 99 | 66 | 0.6 | -3.175 | 0.05059502 |
- x12:
NumberOfPastDue即借款人逾期次数之和 分箱结果
| group | min | max | bad | good | bad_rate | woe | iv |
|---|---|---|---|---|---|---|---|
| 0.0~1.0 | 0.0 | 1.0 | 3424 | 89716 | 0.037 | 0.496 | 0.18318879 |
| 2.0~2.0 | 2.0 | 2.0 | 868 | 2945 | 0.228 | -1.548 | 0.1777373 |
| 3.0~3.0 | 3.0 | 3.0 | 564 | 1167 | 0.326 | -2.043 | 0.168434 |
| 4.0~5.0 | 4.0 | 5.0 | 641 | 817 | 0.44 | -2.527 | 0.2503874 |
| 6.0~19.0 | 6.0 | 19.0 | 456 | 342 | 0.571 | -3.058 | 0.22319805 |
3.2 变量间相关性分析
在进行变量选取前,我们先确定下变量之间是否存在共线性,若存在高度相关性,只需保存最稳定、预测能力最高的那个即可。
这里,我们通过皮尔逊积矩相关系数来确认各变量之间是事存在共线性。
在统计学中,皮尔逊积矩相关系数(英语:Pearson product-moment correlation coefficient,又称作 PPMCC或PCCs, 用r表示)用于度量两个变量X和Y之间的相关(线性相关),其值介于-1与1之间。 通常情况下通过以下相关系数取值范围判断变量的相关强度:
这个相关系数也称作“皮尔森相关系数r”。 皮尔逊系数的定义: 两个变量之间的皮尔逊相关系数定义为两个变量之间的协方差和标准差的商
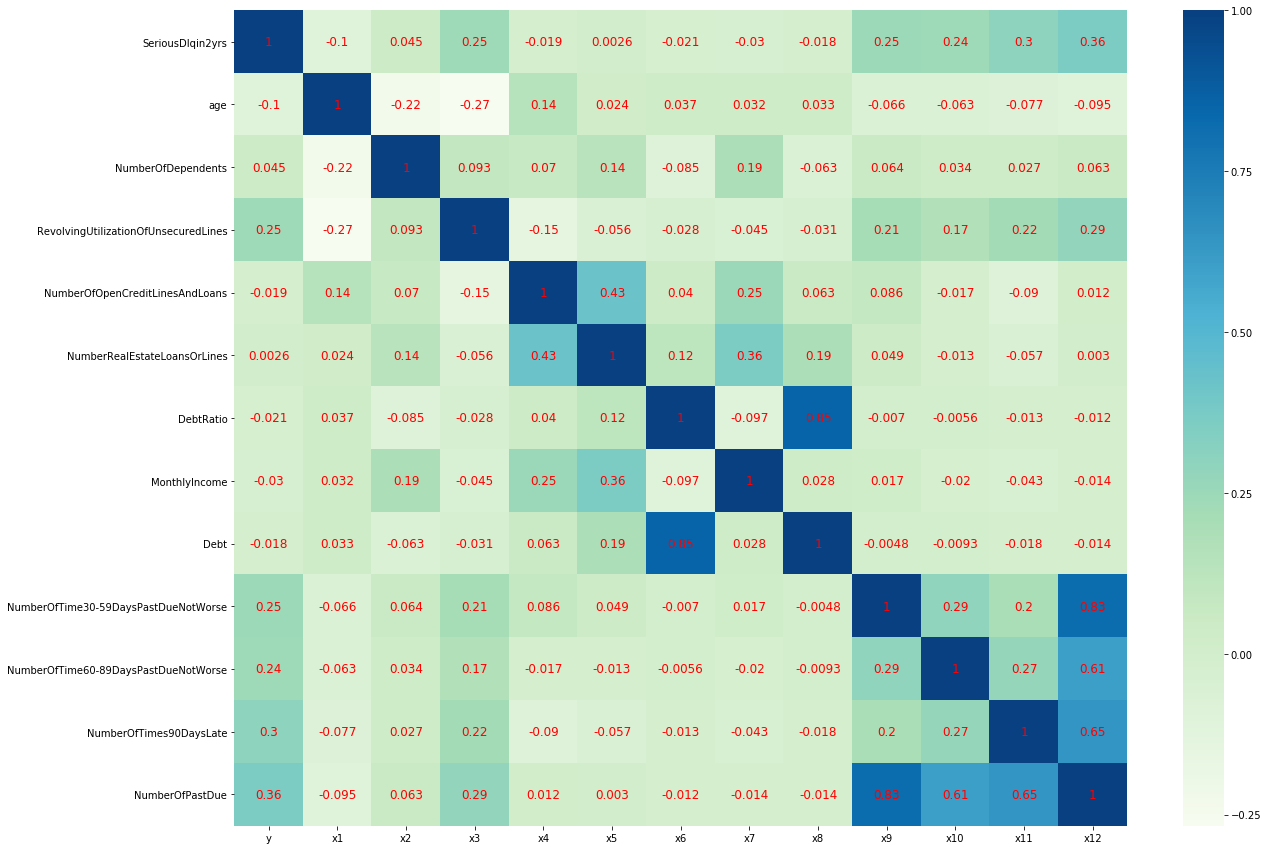
从以上相关系数矩阵与热力图可以发现:
Debt和DebtRatio的皮尔逊积矩相关系数为0.85,极强相关NumberOfPastDue和NumberOfTime30-59DaysPastDueNotWorse、 NumberOfTime60-89DaysPastDueNotWorse、 NumberOfTimes90DaysLate存在强相关或极强相关的关系NumberOfOpenCreditLinesAndLoans和NumberRealEstateLoansOrLines的皮尔逊积矩相关系数为0.43,中等强度相关- 除以上变量外,其余自变量之间弱相关或微弱相关或不相关
通过观察其实可以发现,以上强相关或者极强相关的变量是存在因果关系的。如Debt变量是由DebtRatio变量与MonthlyIncome相乘得到的; NumberOfPastDue变量是由NumberOfTime30-59DaysPastDueNotWorse、
NumberOfTime60-89DaysPastDueNotWorse、
NumberOfTimes90DaysLate三个变量相加得到的。
强相关或极强相关的变量,如果一起放入模型中,会产生共线性(Collinearity)问题,降低模型的预测能力,甚至出现与预测结果相反的现象。
对于强相关或极强相关的变量的处理方法一般为仅保留预测能力最高的一个。
3.3 变量IV值(信息价值)比较
| IV值 | 预测能力 |
|---|---|
| < 0.02 | 无预测能力 |
| 0.02 ~ 0.1 | 弱预测能力 |
| 0.1 ~ 0.3 | 中等预测能力 |
| 0.3 ~0.5 | 强预测能力 |
| > 0.5 | 可疑值或者完美到令人难以置信 |
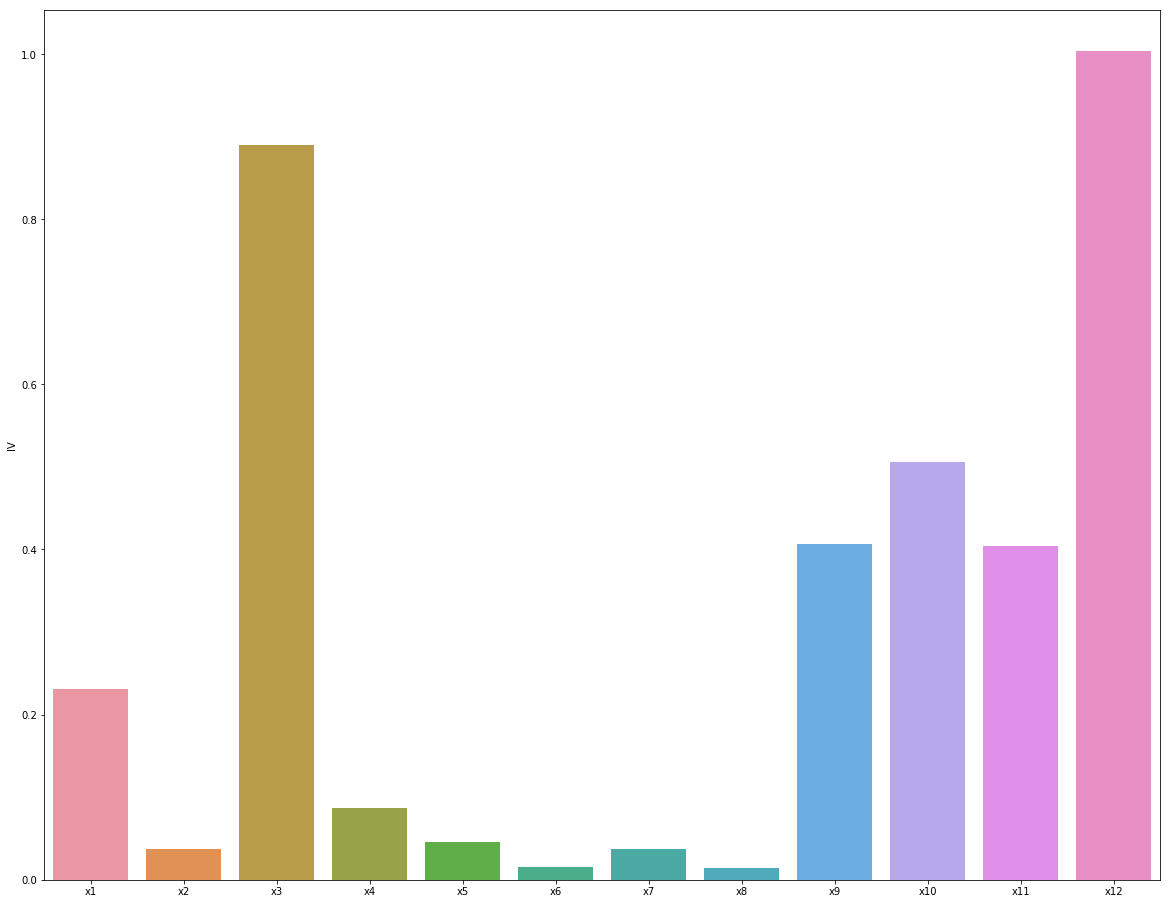
通过以上步骤,我们已经计算出了各个变量的IV值,IV值 的大小将作为我们衡量变量预测能力的量化指标。根据经验,IV值在0.1~0.3之间的才有中等预测能力,这里我们将IV值>0.1的变量作为具有预测能力的特征变量。
如此以来,看下我们选出的特征变量情况:
| 变量名 | iv值 |
|---|---|
| NumberOfTime30-59DaysPastDueNotWorse | 1.00295 |
| Debt | 1.00295 |
| RevolvingUtilizationOfUnsecuredLines | 0.89019 |
| NumberOfPastDue | 0.23158 |
| NumberOfTime60-89DaysPastDueNotWorse | 0.23158 |
| NumberOfTimes90DaysLate | 0.23158 |
| Age | 0.23158 |
| NumberOfOpenCreditLinesAndLoans | 0.08671 |
| NumberRealEstateLoansOrLines | 0.04616 |
| MonthlyIncome | 0.03685 |
| NumberOfDependents | 0.03673 |
| DebtRatio | 0.01595 |
我们的挑选原则为: 从变量列表中筛选IV值>=0.1的的变量,且对于强相关或极强相关的变量只保留IV值最大的一个。
4 特征变量选取结果
按照既定的原则:**从变量列表中筛选IV值>=0.1的的变量,且对于强相关或极强相关的变量只保留IV值最大的一个 **。
但是考虑到这个数据源给的字段较少,如果过少的变量可能会导致模型的预测能力降低。为了尽可能多地涵盖数据集,我们将挑选原则放宽,设定为:**从变量列表中筛选IV值>=0.08的的变量,且对于强相关或极强相关的变量只保留IV值最大的一个 **。
最挑选出了7个变量,变量列表如下:
| 变量编号 | 变量名 | iv值 |
|---|---|---|
| x9 | NumberOfTime30-59DaysPastDueNotWorse | 1.00295 |
| x8 | Debt | 1.00295 |
| x3 | RevolvingUtilizationOfUnsecuredLines | 0.89019 |
| x10 | NumberOfTime60-89DaysPastDueNotWorse | 0.23158 |
| x11 | NumberOfTimes90DaysLate | 0.23158 |
| x1 | Age | 0.23158 |
| x4 | NumberOfOpenCreditLinesAndLoans | 0.08671 |
5 结语
这一周的每一天下班的晚上几乎都花在了这个评分卡的特征工程上,这个过程中查阅了很多资料,正好赶上双11,在京东上买了一本《数据化风控-信用评分卡建模教程》,恰好排上用场。这本书偏重实战,而且是基于真实的业务,比纸上谈兵要更实用一些。
还是学到了很多东西。因为自己的目的很明确,就是要通过个过程了解什么是真正的评分卡,以及这个评分卡建模到开发是怎么样的一个流程,所以对这个过程中应用到的一些最优化分箱算法只是在理论上了解了算法大致原理,并未深入。
但有得必有失,如果一直纠结于去彻底掌握算法上,估计这个系列文章要一直延后了,也与当初的初衷相悖了。
不过如果真的是搭建一个用于业务上的评分卡,特征工程这一块是需要产品经理、风控人员以及数据源提供方不断沟通讨论才能最终确定的,毕竟有些变量的取舍不能仅仅依赖算法,还要结合对业务的理解。
好了,最终要选入模型的短变量列表已经确认,下面可以始通过模型训练数据了。